If you have been on Twitter, you have probably seen pictures like this:
This is Wordle, an addictive little game where the goal is to work out the five letter word in six guesses or less. There is one Wordle a day.

Guesses tell you something about the solution:
- Green means the solution has that letter is in that position.
- Yellow means that letter is in the solution, but not in that position.
- Black usually means that letter is not in the solution at all. (More correctly, black means that letter is in the answer fewer times than you guessed. Look at the first guess ‘TREES’ in the image above. The first ‘E’ is coloured yellow but the second is black. That tells you the answer has exactly one E.)
There is one other rule. Guesses have to be a word (in English). You cannot guess ‘AEIOU’.
I’ve played Wordle for about two weeks, I have settled on the same first word each time. It seems to work pretty well, but I got to wondering whether I could do better. I wanted to know two things:
- What is the best word to use as the first guess?
- What is the best strategy for making the second guess? I’ll explain the choices in a moment.
Yesterday, I decided to find the answer. I downloaded a dictionary and extracted the five-letter words. There were 4,622 of them in all, a number small enough to make brute force viable. I would get my answers by trying every possible combination of answer/first guess/second guess. Or so I thought.
What does ‘best’ mean? For this analysis, I defined ‘best’ as the guess words or strategy which leaves the smallest number of possible answers after each guess, on average.
This post is the story of a day’s effort to find an optimal strategy for Wordle. And I think I found it, a clear but surprising strategy. Skip straight to the conclusion to find it if the details don’t interest you. I’m not absolutely certain this is the optimal answer. If it is not, it is probably close. YMMV.
If this sounds like a great way to take all the fun out of a game, well for me it’s was opposite. This was all great fun.
Getting started
To work out the best word combinations or strategy for Wordle, I need to calculate the number of possible words from any combination of answer and guesses.
The first thing to do, after downloading a list of words, was to write a Wordle colouring function. The function takes a guess and answer as input and returns the Wordle letter colours as a string, for example “12213” with 1 = green, 2 = yellow and 3 = black.
Next, I wrote a function takes a guess (e.g. “HELLO”) and Wordle colours as inputs and then turns that into useable information about the solution. That information is a set of constraints, for example “the second letter of the answer must be E” and “the fifth letter cannot be Y,” etc.
These constraints can then be applied to the list of 4,622 five-letter words. Any word which does not satisfy all of the constraints is excluded. The list of remaining words at the end of that process is the number of possible answers for that guess/Wordle colour combination.
So, for example, if my guess/Wordle combination tells me the four letter of the answer is ‘A’, I can exclude all words in the list of 4,622 which do not have ‘A’ as their second letter.
The guess/Wordle combination tells us about the position of letters in the answer and the how many times a letter appears in the answer:
Position:
Green letters mean that letter is in that position in the answer.
Yellow letters mean that letter is not in that position in the answer.
Number:
A black letter tells you the exact number of times that letter is in the answer. It is equal to the number of times that letter appears in your guess as yellow or green. In most cases, this is zero, so a black letter is not in the answer. However, guesses which include a letter more than once can reveal more. If the guess is “TREES” and one E is yellow and one is black, then we know E appears exactly once in the answer. If both ‘E’s were black then we know there are zero ‘E’s in the answer. If both were any combination of yellow or green then the answer would have exactly two ‘E’s.
Any green or yellow letters which have no equivalents coloured in black gives us the minimum number of times that letter appears in the answer.
With these functions working and tested, it was on to trying out combinations of answer/guesses to find the first guess word that on average produces the smallest number of possible answers.
Question 1: What is the best first word?
Every Wordle starts blank and we have (almost) no priors about the answer. The game is not strategic in any sense, at least in the first round. So in principle the optimal strategy is probably going to use the same first word each time since we start each game without about the same information. But which word?
I can think of three reasons why this same-first-word-strategy might not be quite true. We start with at least some information about the answer because (probably) the game is designed not to re-use answers. We may also learn something about the distribution of answers (i.e. how Wordle is choosing answers), or the set of possible answers. Does Wordle choose common five-letter words more often? If it does, that is going to affect the optimal first guess.
Another possibility is that the game uses the optimal first word as its answer in a puzzle. If that ever happens, then that word will probably (though not certainly) cease to be the best first guess (assuming the system does not re-use past solutions).
To find the best first guess word, I wanted to try every possible guess against every possible answer, both drawn from my list of 4,622 words. For each guess/answer combination, I would do the following:
1. Calculate the Wordle colours, then
2. Use the combination of guess/Wordle colours to calculate the constraints (position and letter number), and finally
3. Apply those constraints to eliminate words from the list of 4,622.
This gives me the number I am interested in: the number of possible solutions left after I have made my first guess. The best word is the one which leaves me with the smallest number of possible answers after the first guess, on average.
Given a set of 4,622 words, there are about 18 million combinations of guesses and answers. To go through every one would take my ageing laptop 33 hours.
But I don’t need to try every possible first guess. Some first guesses are going to be better a priori candidates than others.
I suspect that the optimal first guess probably has no repeated letters. Wordle requires figuring out which letters are in the answer word, and then finding their position. There are 26 letters but only five positions, so the bigger problem is finding the letters. It is probably optimal to cast the widest possible net early on with words that have no repeated letter.
The first guess should also probably have the most common letters in it. I get the distribution of letters in the list of 4,622 five-letter words (not the whole dictionary), then assign a score to each word based on the frequency of the letters it uses. I exclude any words with repeated letters, then sort the list according to its letter score with the highest score first.
Here are the top ten words in that list (by the way, the best first guess word is not in this top 10):

I should say something about distribution. My analysis assumes Wordle picks its answers uniformly from the set of possible words. At the start of my analysis yesterday morning, I worried that Wordle might favour more common five-letter words. That would skew things, possibly a lot. But then I found the solution to yesterday’s puzzle was ‘REBUS’ which makes me think common words do not get special treatment from Wordle. But who knows.
I checked my assumptions about no duplicated letters and common letters by running tests over a sample of possible answers. I tested all possible guesses (all 4,622 of them) but only against random samples of answers. These tests confirmed that words with repeated letters are bad first guesses. One duplicated letter produces about double the number of possible answers compared to words without repeated letters. Words with two repeated letters produced four times more possible answers.
This test also suggested the worst possible word to use as a first guess is ‘MUMMY’.
Out of these tests I pulled the top 98 guess words from my list, sorted by letter distribution, to run against the comprehensive set of possible answers (I don’t know why 98, I think 99 was the first word on my list with duplicated letters, so I stopped there).
And here is the result. The best word to use as a first guess in Wordle is: TARES
As a first guess, TARES produces on average 83.4 possible words. Here is the top ten:
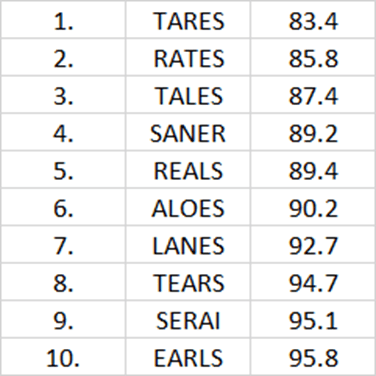
What strikes me about this result is the lack of vowels. Until now, I have been using “ADIEU” as a first guess (how much French is in Wordle?). Most of the top ten words only have two vowels. Go figure.
This result is based on a sample of the best 98 candidate first guesses. That number is too small to give me total confidence that I have not excluded a better answer. I have a bit more work to do yet.
Question 2: What is the best strategy for the second guess?
So we have our first guess. The question now is whether and how to use the information which is revealed by the first guess.
This choice is less obvious than it may first appear. The first guess is going to tell us about some of the letters in the solution and it will say something about their positions. It seems obvious that we should use that information to refine our second guess.
But using that information comes at a cost of re-using letters we already know about, rather than discovering new letters we did find with the first guess.
There is a trade-off between discovering new letters versus finding the position of letters we know are somewhere in the answer, or limiting our choices to the smaller set of possible solutions.
The question is whether it is better to ignore what we learn from the first guess and try a completely new word, knowing it is wrong; or is it better to use the information from the first guess to improve our second guess?
To test this, I ran two second-guess scenarios:
- The ‘naïve’ scenario ignores the information returned from the first guess and makes a second guess with five new letters.
- The ‘strategic’ scenario (I couldn’t think of a better name) incorporates information from the first guess by limiting second guesses to the set of possible answers implied by the first guess. So, if the first guess revealed the second letter is ‘A’ then the in this scenario the second guess will always have ‘A’ as its second letter.
For both of these scenarios, second guesses always follow the optimal first guess, which is TARES.
As in the analysis of first guesses, the goal is to find the strategy which produces the smallest number of possible answers after the second guess, on average.
Naïve scenario
To test the naïve scenario, I pulled from of the list of 4,622 words all the words which have no letters in common with TARES. There are only 267 of these words. This makes up the possible set of second guesses in the naïve scenario. Because the naive scenario ignores the information from the first guess, our task in this scenario is to find the single word which best follows TARES each and every time.
Here is what I did to find this word:
1. For every possible answer (all 4,622 of them), I make a first guess of TARES and calculate the Wordle.
2. From the list of possible second guesses (words which have no letters in common with TARES), and regardless of the first guess result, I choose a word, then calculate the Wordle for this second guess.
3. I then work out the number of possible answers by calculating and applying the constraints from the first guess/first Wordle combination to the list of 4,622, then to that shortened list I apply the constraints from the second guess/second Wordle combination.
This gives me the information I need, the number of remaining possibilities for that first guess/second guess combination.
Here is what I found. The best second guess word to use is: BLOND
So, under a naïve approach which ignores information from the first guess, the best-performing combination of first and second guesses is TARES/BLOND. On average, this combination leaves 7.5 possible words after the second guess. Here are the top ten second guesses following a first guess of TARES.

Having found this TARES/BLOND combination yesterday, I was keen to try it out on today’s Wordle. It worked about as well as it possible: after the second guess, TARES/BLOND left only one possible answer as solution for today’s Wordle: BOOST.
Awesome.
Strategic Scenario
The challenge has been set. The question is whether and in what circumstances is it better to use the information from the first guess in the second guess. The mark to beat is 7.5 average possible answers after the second guess.
The second guess in this scenario is conditioned on the information we glean the first guess. As a result, we are not looking for a single word as a second guess. Instead, we are looking at the average performance of using first guess information to inform the second guess compared to TARES/BLOND no-matter-what.
I suspect this strategy in this strategic scenario is going to perform better the more yellow and green letters turn up in the first guess. I also suspect a mixed strategy might be best: if there is a lot of green and yellow in the first guess, don’t ignore it. Otherwise, go BLOND.
Given this hunch, I decide to keep separate results according to the number of yellow and green letters revealed by the first guess, rather than just report an overall average.
Here are the steps in this second scenario:
1. For every possible answer (again, all 4,622), I make a first guess of TARES and calculate the Wordle.
2. Given the result of the first guess, I make a list of all possible answers and choose my second guess from this list. This means that if the first guess reveals ‘A’ as the second letter of the solution, my second guess is only going to use words which have ‘A’ as their second letter.
3. For each result of the second guess, I calculate the number of possible answers, then add that number to the green/yellow combination from the first Wordle (this will make more sense in a moment). I also keep a count of the number of times each green/yellow combination appears.
At the end of this calculation, having gone through every possible answer/second guess combination (with TARES always as the first guess) I calculate the average number of possibilities for each second guess for each green/yellow combination from the first guess. These results can be compared with the results to the performance of the naïve strategy using TARES/BLOND.
Here is the result:

At first, I did not believe this result. While it confirmed the intuitive finding that the more green and yellow letters there are in the first guess, the better it is to use that information.
But is it really that bad to get three green letters and no yellows on the first guess? Does that combination really deliver 29 possible words on average after the second guess? And are three greens on the first guess really worse than no greens or yellows at all?
Digging a little deeper, it turns out the three greens performance is being largely driven by words ending in ‘es’. There are a lot of five letter words which have a vowel as the second letter ending in ‘es’. To check this, I re-ran the strategic scenario but excluded any results from words ending in ‘es’ and which produced zero yellow letters in the first guess. Sure enough, three greens are much more useful when the solution happens not to be word ending in ES.

As if to confirm how strangely unhelpful three greens on the first guess is, I stumbled across this on Twitter this morning:
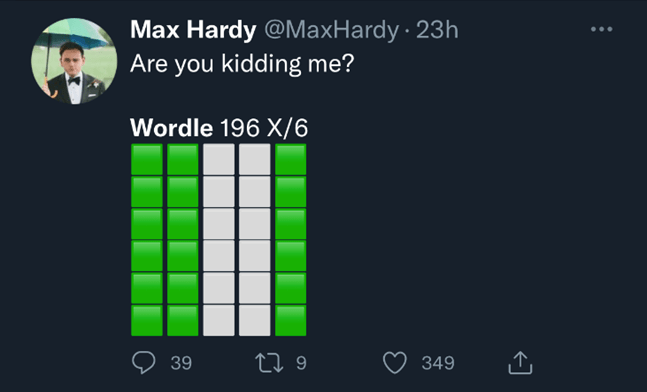
I feel his pain. But perhaps this result is more likely than it seems – that is, if you get three greens in the first place. That probably does not happen very often, I reckon about 1.2% of the time (again, subject to on how Wordle chooses its solutions and also how people choose their guesses).
Some caveats
I’m not sure it’s really necessary to have caveats. This was a day long project and a heap of fun to do. It’s the holidays. I haven’t had a chance to really look at this properly, or to really test the code. The winners only won narrowly and further analysis could change things. I have not checked for similar work, who knows what others have found. The big caveat, though, is distribution. If Wordle is choosing common or obvious five-letter words more often than others, then some or all of this goes out the window. I don’t know if they do.
Apart from that, if these results are wrong, my instinct after all of two weeks playing this game is that it is not by too much. That three greens result bothers me, though.
Conclusion: Optimal Wordle strategy
Based on this analysis and all the assumptions in it, here is the optimal Wordle strategy:
First guess: TARES
Second guess: unless your first guess has four or five green and/or yellow letters, your second guess should always be BLOND.
If Wordle ever uses TARES as an answer, then change your first guess word. Try another word from the top ten above.
Happy New Year!
Interesting! I’d been using “atone”, but that was based on my memory about “etaoin shrdlu” being the most common letters in English, in order. Further research suggests that this may not be true in general, and it sounds like it’s really not true when restricting yourself to a uniform distribution over 5-letter words. Where did you get your word list from?
A slight quibble: “If both were any combination of yellow or green then the answer would have exactly two ‘E’s.” Geese.
I wonder if your results would be any different if you tried to minimize the expected Shannon entropy (base-2 logarithm of the size) of the set of remaining possible words, rather than the expected size of the set.
Also, have you ever seen the answer being a regular plural noun (like “tales”) or third-person singular present-tense verb (like “rusts”)? I’ve only been playing for a week, but I haven’t seen any yet, though they’re certainly accepted as guesses.
LikeLike
Another minor quibble: “Given a set of 4,622 words, there are about 18 million combinations of guesses and answers.” I get over 21 million. Are you sure you didn’t square 4266 or something similar?
And a suggested optimization:
For each guess:
1. Initialize an array with one entry (initially 0) for each of the 3^5 possible colour combinations.
2. For each possible answer:
a. Calculate the colour combination for that combination of guess and answer.
b. Increment the entry of the array corresponding to that colour combination.
3. Each entry of the array now contains the number of possible answers, given that combination of guess and colour combination.
4. Use the array to calculate the expected size or Shannon entropy of the set of possible answers after that guess.
LikeLike